关于我 学术 文字 音乐

王若愚

人工智能科研狗，万众创业打工人，猫狗双全铲屎官，文理双修键盘侠

履历 项目 论文 专利 想法

Horn Clause等价性问题

2021-07-09

tags: Horn Clause, 等价性, 图同构, 知识库

在进行Inductive Knowledge Base Summarization（KBS）的时候发现了一个Horn Clause等价性问题。这个问题来源于对重复构造的Horn Rule的重复性剪枝判断。这个问题我最近发现其在Relational Databases和Deductive Databases中有过相关研究。一条Horn Clause（或称为Horn Rule）其实就是一条Conjunctive Query，因为其指明的条件都是合取连接的。根据已有的理论结果，判断两条Conjunctive Query等价性（Equivalence）和包含性（Containment）的问题复杂度都是NP-Complete[Chandra & Merlin,1977]。但是，Conjunctive Query等价性问题和我在研究KBS时碰到的Horn Clause等价性有一些不一样的地方，因此结论也不太相同。具体来说，有以下几点：

  1. Conjunctive Query对应的Horn Clause要求Head中的所有变量都在Body中出现过，但是在KBS中并非如此，Head中可以包含只出现一次的变量。
  2. Conjunctive Query等价性的定义是，两条query在任何数据库上执行的结果都相同（一般采用Fixed-point语义），query中可以出现一些冗余或者无关的谓词，但是在KBS中，由于top-down+beam search挖掘算法的特性，只关注结构相近长度相同的Horn Rule。 根据KBS的特性，新定义的Horn Clause等价性问题（Syntactic Equivalence of Horn Rules，SEHR）计算复杂度与图同构问题（Graph Isomorphism，GI）相同。

1. 定义

Def #1 Syntactic Equivalence of Horn Rules, SEHR, Horn Rule语法等价性

对于两条Horn Clause \(r_1\)和\(r_2\)，如果存在一种变量的重命名操作\(\theta\)且\(\theta\)为双射，使得\(r_1\)和\(r_2\theta\)在形式上完全一致，那么称\(r_1\)和\(r_2\)是语法等价的。

例如：

\[\begin{equation} h(X, Y) \gets p(X, Y)\label{eq:first} \end{equation}\] \[\begin{equation} h(Y, X) \gets p(Y, X)\label{eq:second} \end{equation}\]

存在一个变量重命名的操作：\(\theta = \{X \mapsto Y, Y \mapsto X\}\)使得\eqref{eq:second}和\eqref{eq:first}完全一致，则两者语义等价。

Def #2 Horn Clause语法等价性判定问题

对于两条Horn Clause \(r_1\)和\(r_2\)，如果存在变量的重命名操作\(\theta\)，使得\(r_1\)和\(r_2\theta\)语法等价，那么返回\(True\)，否则返回\(False\)。

2. 分析

SEHR可以与GI相互在多项式时间内规约，因此可以证明二者的复杂度是相同的。

Def #3 Graph Isomorphism, GI, 图同构问题

\(\mathcal{G} = \langle \mathcal{V}, \mathcal{E} \rangle\) 与 \(\mathcal{G}' = \langle \mathcal{V}', \mathcal{E}' \rangle\)是两个无向图. \(\mathcal{G}\)与\(\mathcal{G}'\)同构当且仅当存在一个双射\(f: \mathcal{V} \rightarrow \mathcal{V}'\)，使得\(\forall u, v \in \mathcal{V}, (u, v) \in \mathcal{E} \Leftrightarrow (f(u), f(v)) \in \mathcal{E}'\)。

2.1 GI\(\propto_p\)SEHR

首先将GI规约到SEHR（G2H转换）。为每一个点\(v_i\)创建变量\(X_i\)，将每一条边\(e(v_i, v_j)\)转化为2个谓词\(e(X_i, X_j)\), \(e(X_j, X_i)\)并将其加入Horn rule body，最后添加一个固定的head：\(h(c)\)，则一张无向图转换为了一条Horn Rule。在这个转换中，创建了1个常量符号，两个谓词符号，\(\vert\mathcal{V}\vert\)个变量, 以及\(2\vert\mathcal{E}\vert\)个谓词。因此该转换可在多项式（线性）时间内完成。

对于一个GI的实例，\(\mathcal{G} = \langle \mathcal{V}, \mathcal{E} \rangle\) 与 \(\mathcal{G}' = \langle \mathcal{V}', \mathcal{E}' \rangle\)是其中的两个无向图。那么可以分别对两个无向图应用上述G2H转换，得到两条rule \(r\)和\(r'\)，构成了一个SEHR的实例。此规约也在多项式（线性）时间内完成。

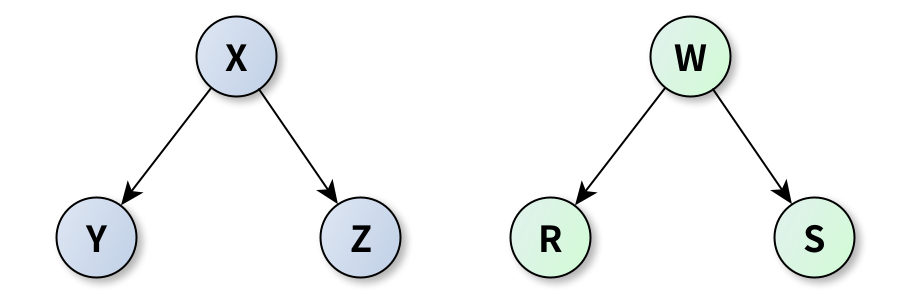
图1. GI → SEHR
图1. GI → SEHR

如图1所示的GI实例可以转换为下列两条Horn Rule构成的SEHR实例：

\[\begin{align*} h(c) & \gets e(X, Y), e(Y, X), e(X, Z), e(Z, X)\\ h(c) & \gets e(W, R), e(R, W), e(W, S), e(S, W) \end{align*}\]

Theorem #4 GI可在多项式时间内规约到SEHR

Proof: G2H转换在图和转换的Horn Rule之间建立了一个双射，因此两图在映射\(f\)下同构当且仅当转换后的Horn Rule之间存在一个变量重命名的双射\(\theta\)使得两条Rule在形式上一致，并且\(f(u) = v \Leftrightarrow u \mapsto v \in \theta\)。 ■

2.2 SEHR\(\propto_p\)GI

接下来将SEHR规约到GI（H2G转换）。从Horn Rule到无向图结构的转换稍微复杂一些。首先，我们需要生成\(k + \vert\Sigma\vert + \vert\mathcal{P}\vert + 1\)个完全子图结构，这些结构将用于表示从0到\(k + \vert\Sigma\vert + \vert\mathcal{P}\vert\)的非负整数（其中\(\mathcal{P}\)表示所有谓词符号的集合，\(\phi(p)\)表示谓词符号\(p\)的元数（arity），\(k = \max_{p \in \mathcal{P}} \phi(p)\)）。非负整数\(i\)用包含\(i+4\)个点的完全图结构表示。例如，整数0和2表示为图2中的两个完全图结构。

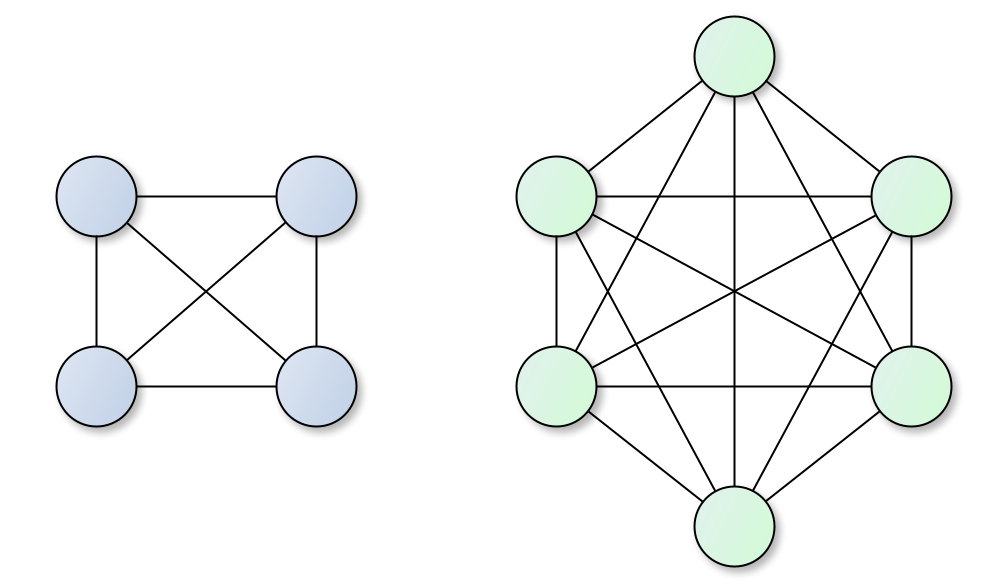
图2. 用于表示整数0和2的完全图结构
图2. 用于表示整数0和2的完全图结构

上述非负整数称为标识符（Identifier），将用于表示谓词中的参数索引以及Horn Rule中出现的常量符号、谓词符号。从0到\(k-1\)的标识符表示谓词中的参数位置（index），从\(k\)到\(k + \vert\Sigma\vert + \vert\mathcal{P}\vert - 1\)的标识符表示常量符号与谓词符号， 而标识符\(k + \vert\Sigma\vert + \vert\mathcal{P}\vert\)则用于标记Horn Rule Head。需要说明的是，如果一个标识符连接到了图中的其他多个子图结构上时，连接处位于标识符结构的同一个节点上。

其次，一个谓词将转换为一个“鱼骨形”结构，其中的一些占位符从表示谓词符号的标识符开始串联起来，用于表示谓词中的各个参数。每一个占位符都和两个结构相连：其一是表示该参数位置的标识符，其二是表示该参数实际取值的标识符或变量节点。如果一个谓词是Horn Rule的Head，则最后的占位符还会和标记Head的占位符相连。例如，图3所示结构表示谓词\(p(X, X, c, Y)\)转化的结构，且该谓词是Head。

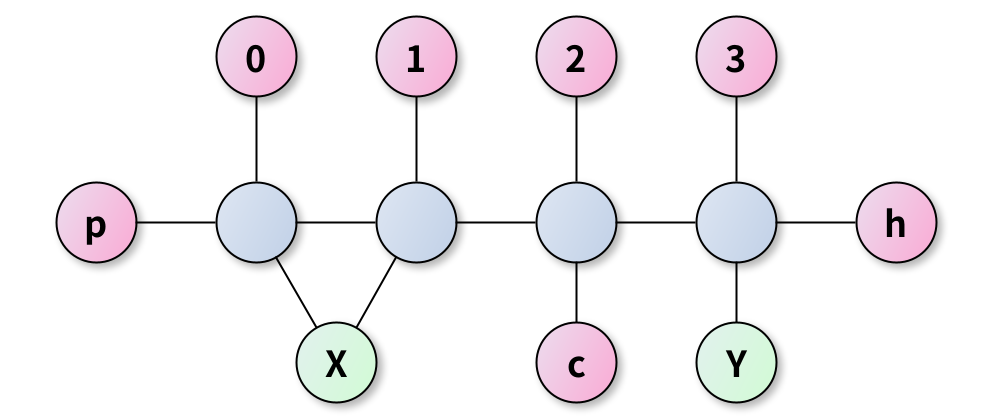
图3. 用于表示谓词p(X, X, c, Y)的“鱼骨形”结构：粉色的圆表示简化的标识符结构，蓝色的圆表示占位符，绿色的圆表示变量。p是一个谓词符号，c是一个常量符号，h是用于表示Head的标识符。
图3. 用于表示谓词p(X, X, c, Y)的“鱼骨形”结构：粉色的圆表示简化的标识符结构，蓝色的圆表示占位符，绿色的圆表示变量。p是一个谓词符号，c是一个常量符号，h是用于表示Head的标识符。

在Rule \(r\)转换后的无向图中，包含\(var(r)\)个变量节点（\(var(r)\)表示\(r\)中的不同变量的数量），\(\Sigma_{P \in r} \phi(P)\)个占位符。令\(s = k + \vert\Sigma\vert + \vert\mathcal{P}\vert + 1\)，所有的标识符中包含了\(O(s^2)\)个节点和\(O(s^3)\)条边。鱼骨形结构中包含了\(3\Sigma_{P \in r} \phi(P)\)条边。因此，这样的转换可以在多项式时间内完成。

令\(r\)与\(r'\)为两条Horn Rule，他们可以通过H2G转换转换为两个无向图\(\mathcal{G}\)和\(\mathcal{G}'\)。需要注意的是，在两条Horn Rule一起转换的时候，\(k = \max_{p \in \mathcal{P} \cup \mathcal{P}'} \phi(p)\)，常量符号的取值范围为\(\Sigma \cup \Sigma'\)，谓词符号的取值范围为\(\mathcal{P} \cup \mathcal{P}'\)。\(r\)和\(r'\)中出现的相同符号应当对应为相同的标识符。则一个SEHR问题实例在多项式时间内转化为了GI问题实例。

Lemma #5 如果转化后的GI实例中的两张图同构，则其中的以下结构分别在映射函数中对应：

  1. 标识符
  2. 占位符
  3. 变量符号
  4. Head转换的结构

Proof: 根据H2G的转换定义，在鱼骨形结构中不会存在包含多于3个点的完全图子结构，因为所有的占位符都是串联的，不存在3个及以上互相连接的占位符。因此，如果转换后的两张图同构，则所有的标识符结构在映射函数中互相之间对应。

占位符是图中仅有的连接在表示参数位置的标识符上的节点。因此在同构的图中，占位符互相对应。

同理，表示变量的节点仅与占位符相连，在同构的图中，表示变量的节点互相对应。

由Head转换得到的结构是图中唯一与表示Head的标识符相连的结构。因此在同构图中，表示Head的结构互相对应。 ■

Theorem #6 SEHR可在多项式时间内规约到GI

Proof: H2G转换在Horn Rule和转换的图之间建立了一个双射。根据Lemma 5，变量重命名的方案\(\theta\)可以从同构映射\(f\)中转换得到：\(X \mapsto Y \in \theta \Leftrightarrow f(X) = Y\)，其中\(X, Y\)是转换后的图中表示变量的节点。在这种对应关系下，两条Horn Rule满足SEHR当且仅当转换后的两张图在\(f\)下同构。因此，SEHR可在多项式时间内规约到GI。 ■

Theorem #7 SEHR与GI的复杂度相同

Proof: 由Theorem 4和6可得，SEHR与GI可以在多项式时间内互相转化，因此具有相同的复杂度。 ■

3. 结论

SEHR与GI复杂度相同，而根据现有理论，GI既不是NP-Complete也不是P，对于一般情况而言并没有多项式时间解法。但是对于一些特定的图的结构来说却可以高效判定。在我的研究中，我为Horn Rule设计了Fingerprint结构，通过Hash操作可以高效判定False的情况。具体细节不再展开。