(待解决)梦到的数学题

2019-08-13

tags: 几何, 反射, 待解决

今天午休，梦中与人论道，期间为了证明“单变量的系统也可以非常复杂”之观点，我举了两个几何问题，题目如下。醒来也觉得虽然题设很简单，但是却也并不好解，遂记录之：

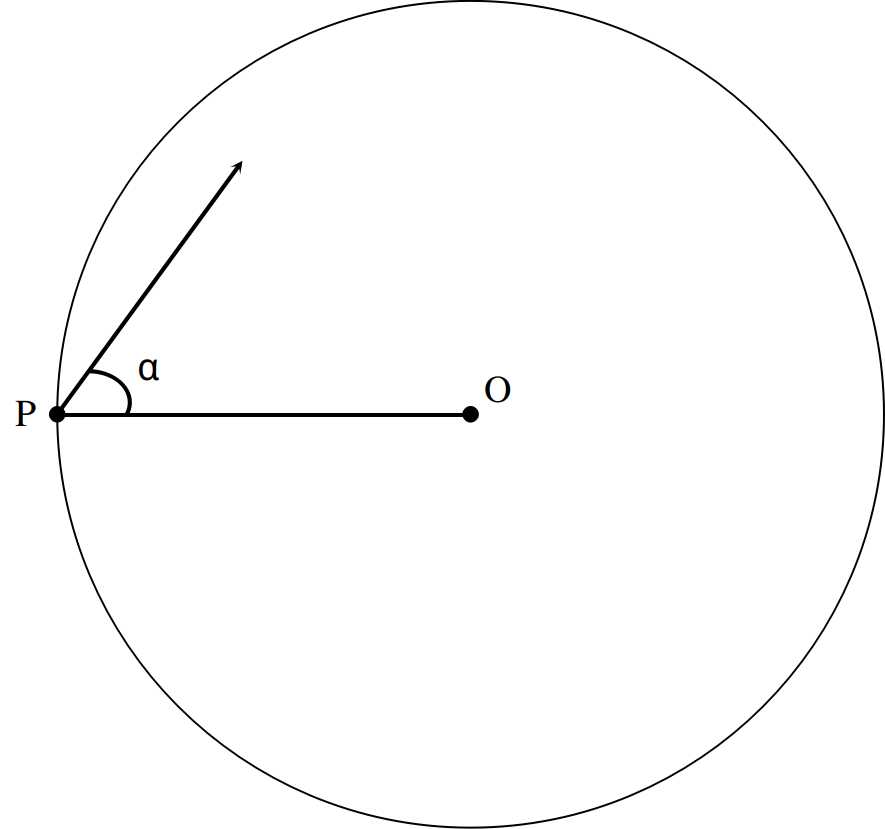
1. 问题一：光线在圆形内的反射

有一个二维的圆形，内部可以反射光线（光线无衰减）其上\(P\)点处有一个激光发射器，向圆内发射激光，发射方向与\(OP\)夹角为\(\alpha\)，问：激光最少经过多少次反射再次回到\(P\)点？

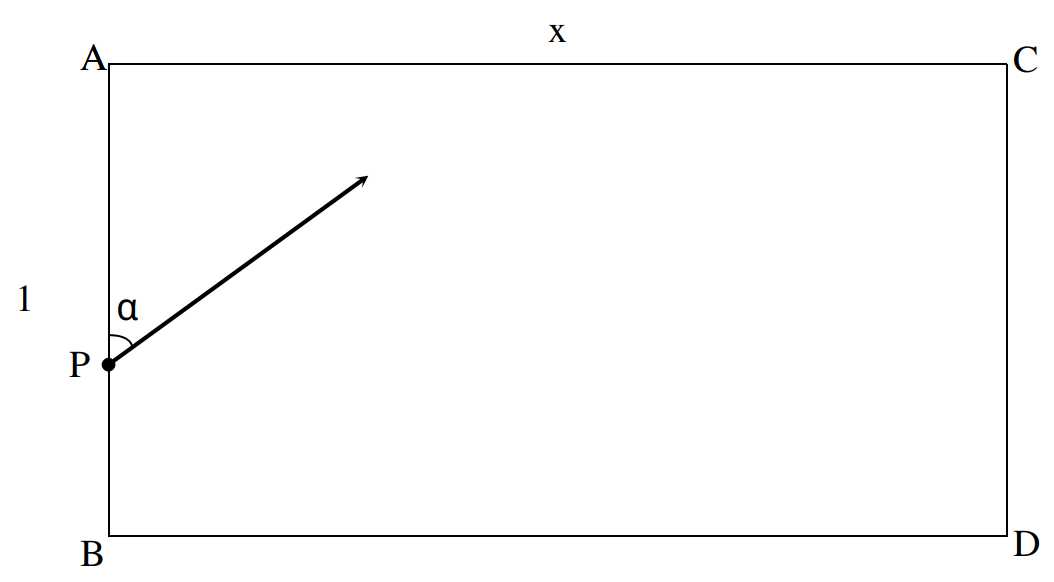
2. 问题二：光线在矩形内的反射

有一个二维的矩形，其中一组对边的长度为\(AB = CD = 1\)，另一组对边的长度为\(x(x >0)\)，矩形的边可以反射光线（光线无衰减）。在边\(AB\)上\(P\)处有一个激光发射器，向矩形内发射激光，发射方向与\(PA\)夹角为 \(\alpha\)，问：激光最少经过多少次反射再次回到\(P\)点？

3. 问题一的解

这一题好解，首先知道激光的方向向上和向下是对称的，因此可以只考虑\(\displaystyle \alpha \in [0,\frac{\pi}{2}]\)。

3.1. 情况1：\(\displaystyle \alpha < \frac{\pi}{2}\)

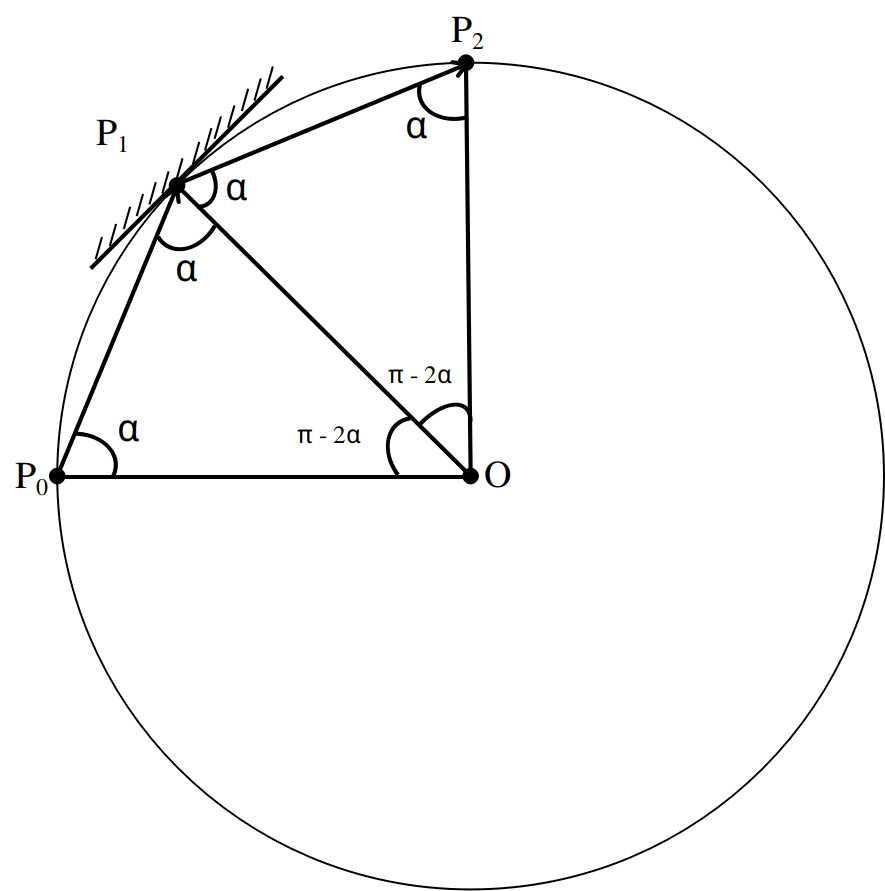
如图3，设\(P=P_0\)，激光射出后的反射点依次为\(P_1, P_2, \dots, P_n\)，则根据等腰三角形及反射原理：

\[\angle OP_iP_{i+1} = \angle OP_{i+1}P_i = \angle OP_{i+1}P_{i+2}= \alpha\] \[\angle P_iOP_{i+1} = \pi - 2\alpha\]

光线回到\(P\)的充要条件为：其转过的圆心角整倍于圆周角，即：

\[\displaystyle \sum_{i=0}^{n-1} \angle P_iOP_{i+1} = n(\pi - 2\alpha) = 2k\pi, k \in \mathcal{N}^+\]

则：

\[\displaystyle n = \min_{\substack{k \in \mathcal{N}^+,\\ 2k\pi \bmod \pi - 2\alpha \equiv 0}} \frac{2k\pi}{\pi - 2\alpha} - 1\]

3.2. 情况2：\(\displaystyle \alpha = \frac{\pi}{2}\)

当\(\displaystyle \alpha \rightarrow \frac{\pi}{2}\)，有：

\[\displaystyle \lim_{\alpha = \frac{\pi}{2}} \angle P_0P_1P_2 = 2\alpha = \pi\]

此时可以认为光线没有传播出去，不符合题设，不予考虑。

3.3. 分析

从情况1可以看出，不是在所有情况下光线都会返回\(P\)点，只有当\(\pi - 2\alpha\)是\(\pi\)的有理数倍时\(n\)才有整数解。此时，设\(\displaystyle \alpha = \frac{b}{a} \pi , a, b, \in \mathcal{N}^+, gcd(a, b) = 1, gcd(b - 2a, 2b) = x\)，则：

\[\displaystyle n = \min_{k \in \mathcal{N}^+} \frac{2k\pi}{\pi - 2\alpha} - 1 = \min_{k \in \mathcal{N}^+} \frac{2bk}{b - 2a} \stackrel{k = \frac{b - 2a}{x}}{=} \frac{2b}{x} - 1\]

4. 问题二的解

暂未完成